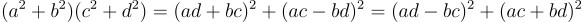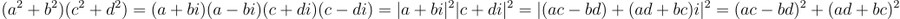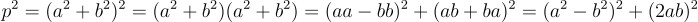수학 정리 이름은 만든 사람이 직접 붙이는 경우 보다는 만든 사람 이름을 따서 다른 사람들이 부르는 경우가 많은데, 이 특성상 한 사람이 여러 업적을 가지고 있으면 이를 구분하기 위해 별명을 만들어야 되는 경우가 종종 있음.
또한, 가능하면 맨 처음 발견한 사람 기준을 하고 싶기는 한데 발견보다는 증명한 사람을 우선시 하는 경우도 있고, 아니면 그냥 다른 사람 유명세에 묻혀서 처음 발견한 사람이 아닌 더 유명한 사람 이름을 따서 불리는 경우도 꽤 있음.
이 페르마의 크리스마스 정리도 비슷한 상황으로, 역사적으로 가장 먼저 출판된 결과는 다른 사람이지만 페르마가 언급한 것으로 더 유명하다보니 페르마의 이름을 따서 부르는 경우가 많음.
그리고 안 그래도 페르마 업적이 좀 있다보니까 그냥 페르마의 정리라고 부를 수도 없는데, 이 정리는 "아마추어 수학자" 페르마의 여타 다른 업적 처럼 정식으로 출판되기 보다는 편지에서 언급된 식으로 알려져 있는데 이 정리가 마침 크리스마스 날짜가 찍힌 편지에 언급된 정리다보니 "페르마의 크리스마스 정리"라는 별명을 가지고 있음.
내용은 꽤 단순한데,
임의의 4로 나누었을 때 나머지가 1인 소수는 두 제곱수의 합으로 나타내진다.
라는 내용임. 우선, 어떤 홀수가 두 제곱수의 합으로 나타내진다면 4로 나눈 나머지가 1이라는 사실은 굉장히 쉽게 보일 수 있음. 그리고, 21처럼 4로 나누었을 때 나머지가 1인 수라도 두 제곱수의 합으로 나타낼 수 없는 경우는 존재함. 그럼에도 불구하고 만약 소수라면, 항상 가능하다는 것이 이 정리가 말하는 바임.
그리고 두 제곱수의 합에 대해서는 재밌는 성질이 있는데, m이 두 제곱수의 합이고, n이 두 제곱수의 합이면 mn또한 두 제곱수의 합임을 쉽게 증명할 수 있음.
이건 그냥 각 변을 전개하면 쉽게 확인할 수 있고, 복소수를 사용하면
같은 식으로도 이해할 수 있음. 이 항등식은 펠 방정식의 해가 무한하다를 증명하는데도 비슷한 형태로 등장하기도 함. 어쨌든 여기에 우리는 소수들에 대해서
1. 2와 4k + 1 꼴의 소수는 모두 두 제곱수의 합임
2. 4k + 3 꼴의 소수는 두 제곱수의 합이 아님
3. 4k + 3 꼴의 소수라도 제곱은 두 제곱수의 합임 (한쪽이 0일 수 있으므로)
라는 사실을 알고 있으므로 이로부터
임의의 자연수를 소인수분해 했을 때 4k + 3꼴의 소수의 인수가 모두 짝수라면 그 자연수는 두 제곱수의 합으로 나타낼 수 있다
라는 사실을 쉽게 알 수 있음. 그리고 여기서 더 놀라운 것은, 이 정리의 역도 성립한다는 점임. 즉, 임의의 자연수가 두 제곱수의 합으로 나타내진다면, 그 자연수의 4k + 3꼴 소인수는 반드시 짝수 차수를 가져야 함. 여기에다가 이렇게 나타내는 방법의 개수 또한 정확하게 계산이 가능하기도 함.
더 나아가서 임의의 자연수는 4^n(8m + 7) 꼴이 아니라면 세 제곱수의 합으로 나타낼 수 있고, 네 제곱수가 있으면 모든 자연수를 나타낼 수 있음.
이러한 사실들의 가장 큰 출발점이 바로 페르마의 크리스마스 정리임. 그리고 이 정리에는 굉장히 짧은 "한 줄 짜리"증명이 존재함.
보면 첫 사각형이 나올 때까지가 증명의 전부고, 나머지 부분은 그냥 증명에 대한 해설에 불과하며, 이 짧은 내용이 논문 전체 내용임. 깨알같이 맨 밑에 참고문헌도 하나 있는 것이 포인트.
증명이 언뜻 보면 복잡하지만 요약하면 역시나 단순한데
1. x^2 + 4yz = p를 만족하는 (x,y,z)의 개수가 홀수개임을 보임
2. 이 때, y,z에 대해서 대칭성이 있으므로 (x,y,z)와 (x,z,y)끼리는 묶어서 생각할 수 있고, 따라서 y가 z와 다른 경우는 짝수개 존재함.
3. 전체 점이 홀수개이므로 y,z가 같은 경우가 반드시 존재하고 따라서 x^2 + 4y^2 = p = x^2 + (2y)^2 가 성립함
이라는 흐름임. 이 증명을 그림으로 더 쉽게 설명하는 내용도 있고, 이 그림 증명을 추가로 해설하는 영상
도 유튜브에 있음.
그리고 이 사실은 피타고라스 순서쌍을 생각하는데도 도움이 되는데, 실제로 p = a^2 + b^2 이라고 한다면 자연스럽게
을 얻게 되고, 이 꼴은 p가 소수여야 한다는 것을 잊어버리면 원시 피타고라스 순서쌍의 일반적인 꼴을 나타내고 있음. 즉,
(3,4,5)
(5,12,13)
(7,24,25)
(8,15,17)
...
같이 원시 피타고라스 순서쌍들을 볼 때 가장 큰 수에 소수인 경우가 꽤 있어 보이는 경우는 우연이 아닌 셈
1. 수학 정리 이름 붙이는 것 보면 은근히 재밌는 것들 좀 있다.
2. 정리 이름이 꼭 정리 내용이랑 상관은 없을 수 있다
3. 메리 크리스마스