투표에 관해서 흔히 "완벽한 민주주의는 불가능하다"로 해석되는 정리가 하나 있음. 애로우의 불가능성 정리라고 불리는데, 그 내용은
3명 이상의 투표자와 3명 이상의 후보자가 있고, 모든 투표자가 모든 후보자에 대한 선호 순위를 가지고 있으며, 이를 바탕으로 최종 선호 순위를 결정하는데
1. 모든 투표자가 A 후보보다 B 후보를 선호한다면 최종 선호 순위에서도 A 후보가 B 후보보다 선호되어야 한다
2. 사람들의 선호 순위가 바뀌었는데 그럼에도 모든 사람들이 A, B 후보 중 더 선호하는 후보는 그대로라면 최종 선호 순위에서도 그 두 후보의 순서는 그대로여야 한다.
3. 독재자가 없다. 즉 모든 사람에 대해서, 자기의 선호 순위와 최종 선호 순위가 일치하지 않는 경우가 항상 존재한다.
라는 조건을 만족하는 최종 선호 순위 결정 방법은 존재하지 않는다는 정리임. 여기서 1. 조건은
임의의 두 후보에 대해서 최종 선호 순위에서 A가 B보다 앞서는 경우도, B가 A보다 앞서는 경우도 존재한다.
라는 조건으로 완화될 수 있음.
이 정리는 저런 충분히 합리적인 조건들을 만족할 수 없다는 내용이 충격적이기도 하고, "독재"라는 강한 단어를 사용하고 있기 때문에 막 "역시 답은 민주주의가 아니라 독재!" 라고 해석하는 경우도 튀어나오고 하는데, 우선 이 정리에 대해 확실하게 짚고 넘어가야할 점은 이 정리는 정치학적인 관점에서 나온 것이 아니라 경제학적인 관점에서 유도된 정리라는 점임.
실제로 선호도에 대해서 "모든 사람이 모든 후보자에 대해 완전한 선호 순위를 가진다"라는, 경제학에서 자주 보이는 "합리적인 선호도"를 전제하고 있는 점에서도 그게 잘 드러남.
또한, 현실에서는 대체로 승자만이 중요하고 나머지 후보자들의 순위는 중요하지 않은 승자 독식 구조나, 아니면 애초에 순위를 넘어서 정량적인 비율이 중요한 비례 대표 구조가 제대로 반영되지 않고, 어디까지나 "완전한 최종 선호 순위"를 매기는 데 중점을 두고 있는 것 또한 정치학적으로 적용되기엔 다소 어려운 점이 있음.
그리고 조건 2의 경우를 보면 "나는 A가 싫으니까 B 좋더라도 C한테 투표하련다!" 하는 전략적 투표 관점이 반영되어 있지 않은 면 또한 있음.
더군다나 실제로 현실에서는 보면 A랑 B 둘 중 누가 낫냐 하면 A라고 대답하고, B, C 중에선 누가 낫냐 하면 B라고 대답하더라도 A, C 중에선 C가 더 낫다고 하는 사람들도 종종 있는데, 이런 경우도 "비이성적인 선호"라는 이유로 배제되어 있기도 함.
그런 의미에서 이 정리는 "독재가 낫다" 라고 말하기 보다는 "민주주의 하는데 있어서 골치 아프게 막 사표 배제할 방법 고민하고 투표 방법 복잡하게 정의하려고 하지 말고 그냥 룰만 모두가 납득할 수 있게 깔끔하게 정의하고 끝내라" 라고 말한다고 해석하는 것이 더 적합할지도 모름. 어차피 순위를 완전하게 결정한다고 해서 권력과 책임을 이에 따라서 나눌 수도 없는 꼴이기도 하니.
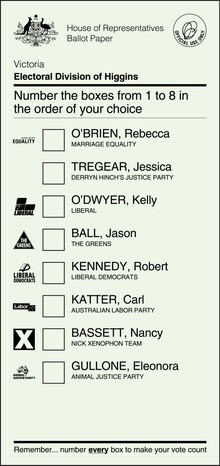
참고로 애초에 저렇게 순위 매겨서 투표하는 경우가 있음? 하고 물어볼 수도 있는데 사실 놀랍게도
호주가 그런 식의 투표 방식을 쓰긴 함.
1. 어느 투표 방식도 완벽하기는 어렵다.
2. 결국 민주주의에 있어서 중요한 것은 시민들의 동의를 얻는 것.
3. 참고로 이 정리 증명한 애로우는 이 업적을 포함하여 다양한 업적을 세웠고, 노벨 경제학상 받음.