(이전 글에서 이어짐)
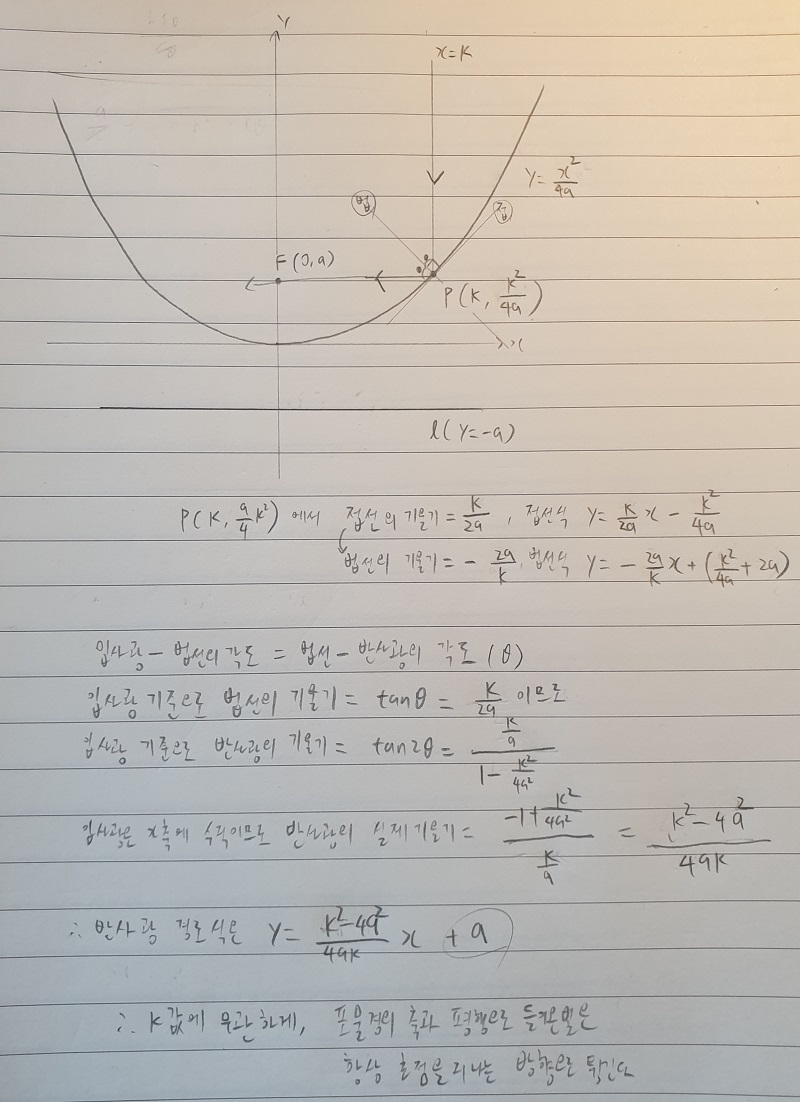
계산해보니까 어때?
왜 생각보다 할만하게 느껴지지?
그야 반사공식은 해석기하학적으로 약간의 미분과 삼각함수의 덧셈공식만으로 해결이 되니깐
노트 한페이지를 빼곡히 써서 유도가 가능하다는 뜻의 약간이면 맞을지도
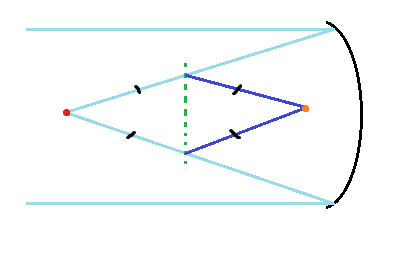
어쨌거나 거울이 포물면이면 깊이에 상관없이 방향만 맞으면 항상 초점에 모이는걸 확인이 가능하지
수학적으로 근사치 없이 정확한 결과기에, 대규모의 정밀망원경들은 항상 거울을 써
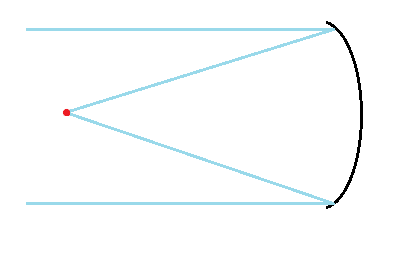
그런데 거울이면 빛이 모이는 곳이 들어오는 곳과 같은 방향이 되지 않아?
그게 반사망원경들의 고질적인 문제야, 모인 빛을 들어오는 곳 밖으로 어떻게든 빼내야 하기에
어쩔 수 없이 빛이 들어오는 곳 일부를 가려야 되거든
같은 구경이면 굴절식보다 반사식이 더 어둡다는게 이런 뜻이었구나
그래서 그 "밖으로 빼는" 과정은 어떻게 되는데?
맞춰봐, 힌트를 주자면 간단할수록 효율적인 방법이야
거울때문에 경로가 꺾인거니, 거울로 한번 더 꺾는다...?
그게 뉴턴이 고안한 방법이지, 비스듬한 평면거울 하나로 해결한거
그래서 대구경 망원경 중에 가장 인기가 높고 가격도 싼게 뉴턴식 반사망원경이야
하지만 옆으로 꺾는거면 처음에 다룰 때 꽤나 고생하겠는걸
맞아, 그래서 보는 방향과 들어오는 방향이 일치하게 만들려는 노력들이 많이 있었지
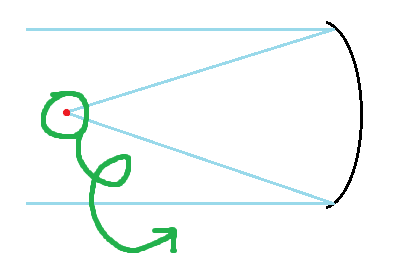
얼핏 생각하면 평면거울을 바로 세우면 될것 같은데.....
그러자니 주경 밖으로 빼려면 절반에 해당하는 면적을 가려야 하는 문제가 생기는구나
저대로 만들면 차폐율이 너무 커져서 힘들게 되지
하지만 튕기는 방향을 똑바로 하는 방향성 자체는 맞아, 그럼 어떻게 하면 될까?
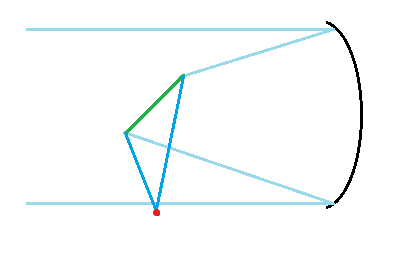
한 점으로 모이는 빛을 다른 점으로 모이게 하는 곡면거울을 쓴다?
그렇게 해서 만들어진게 두 개의 곡면거울을 쓴 반사망원경들이야
한 점으로 모이는 빛을 다른 점으로 모이게 한다는 건, 그 곡선의 '중심'이라고 할만한 점이 두개라는 뜻이지
두 개의 초점!
그리고 두 개의 초점을 가진 도형 중 가장 익숙한 건?
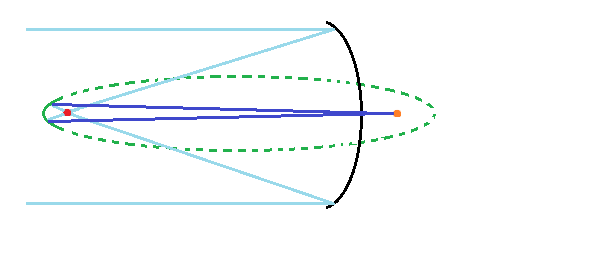
타원이겠지 역시
타원에서 한 초점을 지나는 빛은 어떻게 튕길까?
직관적으로 보자면 반대편 초점을 향해 튕기겠지만, 역시 증명이 문제겠구나
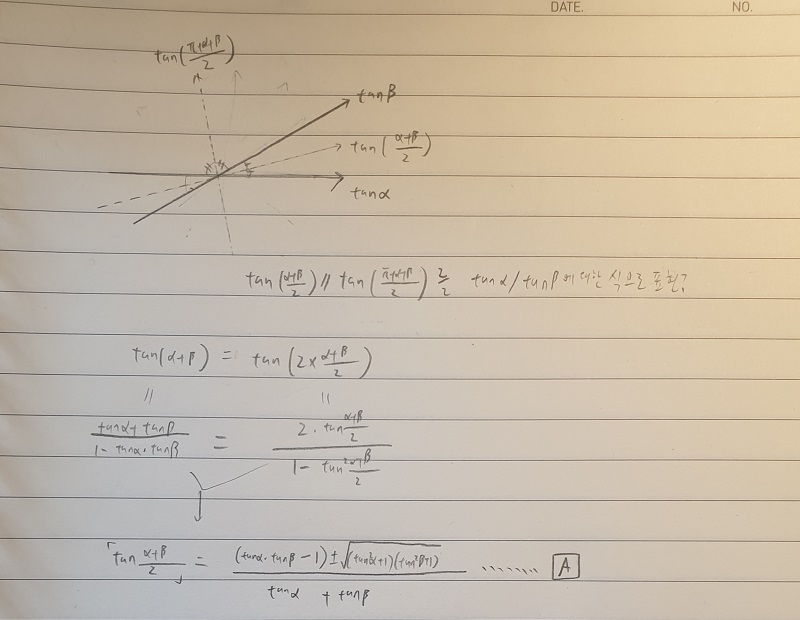
포물선을 뺀 원뿔곡선들의 반사공식을 증명하려면 우선 삼각함수, 정확하게는
탄젠트 함수의 반각 일반공식부터 정리하는게 편해
배각 공식을 뒤집어서 이차방정식으로 풀다보니 근이 두개가 나오는 건가....확실히,
그리고 이걸 타원 위의 점에 대해 대입하면 생각보다는 간단하게 증명을 할 수 있지
직관적인 결과는 알고 있으니깐, 두 경로의 각을 이등분한 직선들이 각각
접선과 법선과 일치한다는 걸 보이는 걸로 증명하는게 포인트야
그런데 이걸 아까 전의 포물면에 적용할 수가 있나?
한걸음 뒤로 물러나봐
한걸음....?
초점을 지나가게 한 다음, 원래 포물면의 초점을 새로운 타원의 초점으로 만드는 거지
아하, 그러면 작은 반사경으로도 나머지 빛을 주경 뒤쪽으로 모을 수 있겠구나
게다가 이 방식은 빛이 초점을 두번 지나가기에 원본과 동일한 정립상을 만들어
그런데 이러면 뉴턴식 반사망원경보다 경통이 더 길어져야 하는거 아냐?
그게 그레고리식 반사망원경의 가장 큰 약점이야, 그래서 소~중구경 내지
주경의 직경 대비 초점거리가 짧은 대구경 망원경에만 쓸 수 있어
분량조절 실패.....다음 편까지 이어서 써야 완결납니다