A : 뭐, 뭐야! 내 꼴짤 어디갔어! 이 이상한 대리석 같은 무늬는 뭐야!
B : 진정하라구 친구. 눈을 잠깐만 다르게 보면... 짠!

A : 그래 이건 내가 원하던 꼴짤이야 으헝헝! 그런데 B, 대체 저 이상한 무늬와 이 꼴짤이 무슨 상관이 있다는거야?
B : 그건 바로 이 짤을 변형시켜 만든게 저 이미지야.
A : 그러니까 그걸 모르겠다고.
B : 상세한 건 복잡하지만, 골뱅이는 알아?
A : 골뱅이가 뭔데? 먹는거?
B : 아, 그거 말고. 골뱅이 찍기. 컴공과라면 대부분 알고 있을 대표적인 알고리즘 문제 중 하나야.
A : (그게 뭔데 씹덕아...)
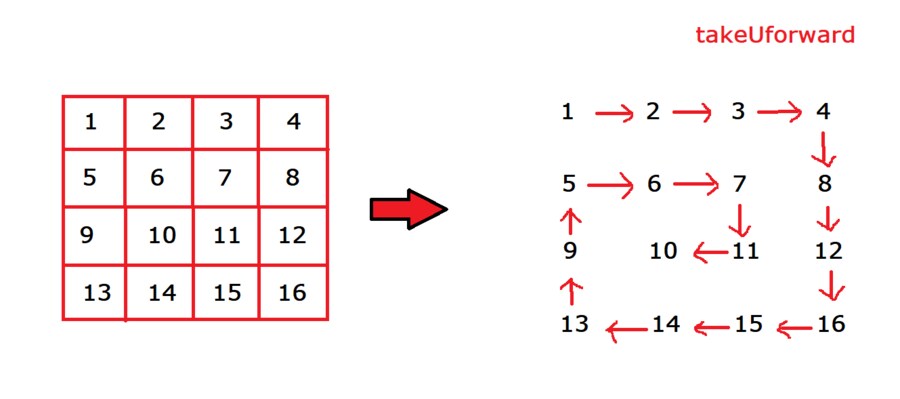
B : 골뱅이 찍기, 다른 말로 Spiral Order, Spiral Matrix라고 불리우는 이 문제는, 왼쪽처럼 행렬이 주어지면, 골뱅이 처럼 꼬불꼬불하게 순서를 지정해서 출력하는 문제야. 구조가 어려워 보이지만, 안될때 방향전환을 해주고 다음 칸으로 움직이게 하면 깔끔하게 해결할 수 있어.
A : 그러니까 원본 이미지에 이걸 적용했다는 얘기야?
B : 응, 맞아. 이 알고리즘을 이용한 순서를 적용한거긴 한데, 실제론 좀 더 복잡하게 만들었어.
A : 왜?
B : 만들어진 패턴이 별로 안이뻐서.
A : (그렇군...)
B : 실제로는, 이 방식을 적용한 뒤, 이미지를 4개로 쪼개서 각 부분 이미지에도 다시 이 알고리즘을 적용해.
A : 그럼 두 번만 하면 된다는거야?
B : 아니, 그 부분 이미지는 다시 전체 이미지로 해석되서, 부분 이미지의 부분 이미지도, 부분 이미지의 부분 이미지의 부분 이미지도..
A : 으악! 알겠어.
B : 이걸 재귀적이라고 하는게 알아듣기 쉬울 수도 있겠네. 아무튼 이렇게 적용하면 이미지를 저렇게 인코딩, 디코딩 할 수 있어.
A : 좋아. 근데 이걸 왜 만든거야?
B : 왜 만들었을까? 후후...

(위 영상은 Windows XP의 대표적인 배경화면 'Bliss'을 해당 방법으로 인코딩 한 것이다. 위의 원본 영상과 비교하면, Bliss의 특징적인 색상 분포가 어느정도 유지되는 것을 알 수 있다. 이는 우리 방법이 픽셀 값을 변경하는게 아닌, 오직 순서만 변경하는 비압축 방식이기 때문이다.)
코드는 'import numpy as np\n\ndef spiral_matrix(n, m):\n matrix = np.zeros((n, m), dtype=int)\n directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]\n current_direction = 0\n row, col = 0, 0\n num = 1\n while num <= n * m:\n matrix[row, col] = num\n num += 1\n next_row = row + directions[current_direction][0]\n next_col = col + directions[current_direction][1]\n if (0 <= next_row < n and 0 <= next_col < m and matrix[next_row, next_col] == 0):\n row, col = next_row, next_col\n else:\n current_direction = (current_direction + 1) % 4\n row = row + directions[current_direction][0]\n col = col + directions[current_direction][1]\n return matrix\n\ndef f2(img):\n h, w, c = img.shape\n img = img.copy()\n if(h <= 1 or w <= 1):\n return img\n img = img.reshape(-1, 3)[spiral_matrix(h, w).flatten() - 1].reshape((h, w, c))\n p0 = f2(img[:h//2, :w//2].copy())\n p1 = f2(img[:h//2, w//2:].copy())\n p2 = f2(img[h//2:, :w//2].copy())\n p3 = f2(img[h//2:, w//2:].copy())\n img[:h//2, :w//2] = p0\n img[:h//2, w//2:] = p1\n img[h//2:, :w//2] = p2\n img[h//2:, w//2:] = p3\n return img\n\ndef inverse_permutation(permutation):\n n = len(permutation)\n inverse = [0] * n\n for i, p in enumerate(permutation):\n inverse[p] = i\n return inverse\n\ndef f2i(img):\n h, w, c = img.shape\n img = img.copy()\n if(h <= 1 or w <= 1):\n return img\n p0 = f2i(img[:h//2, :w//2].copy())\n p1 = f2i(img[:h//2, w//2:].copy())\n p2 = f2i(img[h//2:, :w//2].copy())\n p3 = f2i(img[h//2:, w//2:].copy())\n img[:h//2, :w//2] = p0\n img[:h//2, w//2:] = p1\n img[h//2:, :w//2] = p2\n img[h//2:, w//2:] = p3\n img = img.reshape(-1, 3)[inverse_permutation(spiral_matrix(h, w).flatten()-1)].reshape((h, w, c))\n return img\n\nfrom PIL import Image\nimport numpy as np\nimport matplotlib.pyplot as plt\n\nimage_path = ''\nimage = Image.open(image_path)\nplt.imshow(image)\nplt.show()\n\nimage_array = np.array(image)\nimage_shape = image_array.shape\nprint(image_array.shape)\n\nimage_array = f2(image_array)\nplt.imshow(image_array)\nplt.show()\n\nImage.fromarray(image_array).save(image_path.replace('.','_encoded.'))\n\nimage_array = f2i(image_array)\nplt.imshow(image_array)\nplt.show()' <- 여기!


뭐래
파이썬코드에 개행문자삽입한게 매우 끔찍해요
바꾸기 편하라구 그랬오
긍금한게 이렇게 만든이미지 크기를 2배줄이고 다시 복호화하면 어케됨?
일단 2배 줄인채로 복호화하면 방식 자체가 크기에 따라 재귀 다르게 들어가는 구조라서 복원이 안되고, 2배 샘플링해서 복원하면 복원이 안되진 않지만.. 이렇게 나옴
신기하네
밤샘을한 개발자 인가?