2025의 이 신비해 보이는 성질은
이렇게 잘 알려진 그림으로도 증명할 수 있는데, 이 그림을 보면 굉장히 규칙적이고 실제로 이 성질은 2025만이 가지는 전유물이 아님.
즉 일반적으로,
이라는 성질이 성립함. 또한, 이러한 k승은 예전부터 연구 되었는데, 이 주제에서 파생되는 끝판왕이 바로
리만 제타 함수 되시겠다 이거임. 뭐 여기서 리만 가설 얘기까지 끌고 갈 것은 아니고, 여기서는 저 공식들과 관련된 이야기들만 조금.
우선 저 공식들을 유도하는 가장 원초적인 방법부터 소개를 하자면, 이 방법의 아이디어는 기본적으로 적분에서 온다고 할 수 있음. 즉,
대충 이런 느낌에서 아이디어를 얻는 것. 실제로 위의 공식들의 최고차항들만 보면 정확하게 저것이 나오는 것을 알 수 있음. 이것에서 아이디어를 얻어서 제곱의 합의 공식을 유도해보자면,
이라는 식들을 통해서
을 얻으면 이 식을 정리해서
라는 결론을 얻을 수 있음. f_k(n)을 k승의 n까지 합이라고 하면 이 결론을 쉽게
같은 식으로 일반화할 수 있음. 하지만 이 과정은 식을 계산하는 것이 번거롭고, 매 번 k-1승의 합, k-2승의 합, 등등을 전부 이용하니까 좀 복잡하고 번거로운 문제가 있음.
이 방법을 해소하는 방법 중 하나로는, 가짜 변수를 도입하는 것임. 그 방법 중 하나는
이라는 다항식을 정의하면, x에 1을 대입했을 때 우리가 원하는 합이 되고, 여기에 미분을 도입하면
라는 지극히 단순한 관계식을 얻을 수 있음. 여기서, x가 1이 아니라면
을 얻을 수 있고, 애초에 다항식이 연속인 것을 생각하면 여기서 1로 갈 때 극한을 계산하면 마찬가지로 합 공식을 얻어낼 수 있음. 즉, 이 방법으로
을 유도하는 방법을 설명하자면, 위의 식을 통해서
을 얻고, 여기서 로피탈의 정리를 두 번 적용하면
을 얻어낼 수 있음.
이 방법을 이용하면 아무래도 전 단계만 정확하면 되니까 계산을 좀 더 규칙적으로 할 수는 있게 되는데, 그래도 미분만 하면 되는 게 아니고 매번 x를 곱하고 미분하는 것을 반복해야 하니 여전히 번거로움은 남아있음.
하지만 여기서, 미분이 계수를 규칙적으로 바꾸는 데 사용할 수 있다는 것을 깨닫고 나면
을 사용해서
라는 식을 얻을 수 있고, 여기서 x에 0을 대입하면 우리가 원하는 합을 얻을 수 있음. 즉,
을 얻을 수 있고, 여기서 상수는 미분해도 0이라는 것을 생각하면
라고 변형할 수 있음. 즉 이 방법을 이용하면
이라는 겉보기에 깔끔한 결론을 내릴 수 있음.
사실 이 문제에 대해서는 이게 시작이고 여기에서 이제 베르누이 수와의 연관성이라든가 스털링 수와의 연관성, 바젤 문제 등 할 얘기가 너무 많아서 여기까지는 진짜 도입부에 불과하고, 막 0^0은 1로 보는 것이 좋은가 문제도 조금 얽혀있기도 하는 등 다룰 수 있는 떡밥도 많지만 그런 내용은 이미 다룬 곳도 꽤 있고, 너무 길어질 것 같으니 이번에는 여기까지.
1. 더 많은 내용은 언젠가 있을지도 모르는 Part 2를 기대하세요!
2. 만약 궁금증을 도저히 못 참겠다 싶으면 위키에서 Faulhaber's formula를 검색하면 Part 2에서 아마도 다룰 내용들이 있음
3. 원래 어제 중에 완성하려고 했는데 좀 늦게 시작했다가 어느 새 날짜 넘겨버리기도 했고 길이도 생각보다 길어져서 여기서 컷
4. 내일 제 때 일어날 수 있으려나







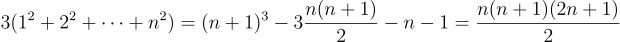

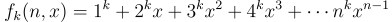
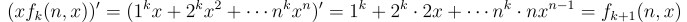
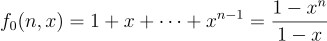
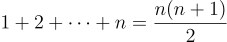
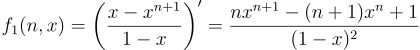
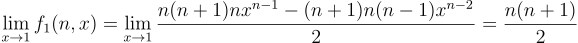
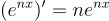
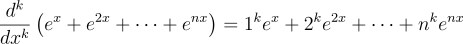
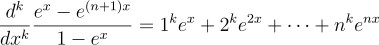
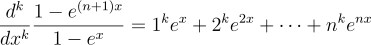
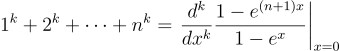
뭔지 모르겠고 그림 이쁘다 헤헤
저 그림은 내가 그린 거니까 마음껏 퍼가서 2025의 신기한 성질! 하는 식으로 글 써도 됨ㅋㅋ
이런거 보면 수학 공부 다시 하거싶엉. 취미 수학 시작해볼까...