반갑노라! 이 몸, 미치르 메르헨! 그대들의 여왕이노라! 접견을 허락하노라! 유하유하!
오늘은 연속체 가설에 대해서 설명하겠노라!
(그냥 엘든링이나 해서 여왕님이 비명지르는거 보고싶은데...)
아무튼! 어느날 게오르그 칸토어 라는 사람은 무한에도 크기가 있을지 생각했노라!
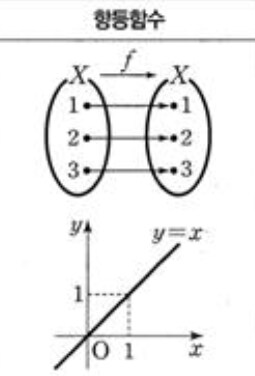
집합 A와 집합 B의 요소들이 서로 일대일 대응 한다면 두 집합의 크기는 서로 같느리라!
예시를 들어서 정수와 자연수의 크기 비교를 해보겠느리라!
0의 자리는 1에 대응시키고
짝수는 음수에 대응시키고 홀수는 양수에 대입시키면 각각 일대일 대응이 가능하노라!
즉, 자연수와 정수의 집합의 크기는 같다는걸 여기서 선포하노라!
(대충 정수안에 자연수가 있는데 그럼 정수가 큰거 아니냐고 하지만
수학과 척척수료 여왕님에게 따지면 밴당할까봐 넘어가는 깃발단)
그럼 이번엔 더 작은 0~1까지의 소수와 자연수의 크기비교니라!
일단 자연수를 번호처럼해서 소수를 쭉 세워 놓느니라!
그런 다음 대각선을 그어서
각 자리수의 수마다 1을 더한 값을 차례대로 쓰느리라!
아참, 숫자가 9면 1을 빼서 8로 만들면 되노라!
그렇게 만든 수를 자연수와 대응시킨 표에서 찾아본다면....없느니라!
적어도 모든 숫자가 대각선 숫자와는 한자리씩은 다르기에
자연수와 일대일 대응시킨 수에는 없다는게 결론이니라!
그래서 0~1사이의 소수의 크기가 자연수의 크기보다 크다는것을 선포하느니라!!
(깃발단의 뇌용량을 초과하여 머리가 깨져버린 깃발단) : 헤..헤헤...샤카샤카밤바스...
자자! 다 왔느니라!
이제부터 연속체 가설을 설명하기 위한 준비가 끝났으니 조금만 더 참으면 되느니라!
이렇듯 칸토어는 자연수, 정수, 홀수, 짝수 등
가장 작은 무한의 크기를 알레프-0라고 부르기로 약속했노라
깃발단 : 아하! 그럼 그거보다 더 큰 실수, 무리수, 복소수 등의 크기든 알레프-1 로 부르기로 한거죠?
미치르 : 그것들의 크기는 2^알레프-0라고 했노라
크아아악!!! 야드 파운드 쓰는거마냥 이 소름끼치는 문자는 뭐냐고!!!
다 때려쳐! 엘든링이나 보여줘요!!!!
(매니져에게 임차당함)
존 벤(벤다이어그램 만든사람) : 어휴, 집합 A의 부분집합의 크기는 2^(부분집합의 갯수)
라는거 고딩때 안배웠니?
그러니까 실수등의 크기는 2^알레프-0가 된거지
어...뭐 아무튼, 여기서 더 첨언을 하자면 칸토어는 대각선 논법으로
멱집합 P(모든 부분집합을 원소로 하는 집합)
ex) A = {빙,구}
P = {Ø, {빙},{구},{빙,구}}
멱집합 P의 크기 > 2^(부분집합의 갯수) 임을 증명했느니라
그래서 자연수보다 큰 실수집합의 농도가 자연수 집합의 멱집합의 농도가 같아
실수의 집합의 크기는 2^알레프-0가 되느니라
노년의 칸토어 : .....흠, 그렇다면 2^알레프-0는 알레프 몇인거지?
알레프-0와 2^알레프-0 사이에 존재하는 기수 x가 존재할까?
아니, 이런 집합은 존재하지 않아! 증명해보이겠어!!
하지만 칸토어가 연속체 가설을 증명하는 일은 일어나지 않았다
거짓말같이 말년에 궁핍과 영양실조로 정신병원에서 생을 마감한다
깃발단 : 저런...그럼 연속체 가설은 미해결 문제로 남은거에요?
아니? 해결은 되었느니라. 그런데....
쿠르드 괴델 : 야레야레... 또 공리계에서 반증불가능한 논제에 대해서 논하는건가요 못말리는 여왕님?
그렇다면 우리는 불완전성의 정리를 던질거에요
저 이야기를 하려면 엄청 길어지니 다음편에서 하자꾸나....
그대들 오늘도 즐거웠고, 이만 물러가도 좋도다!
안돼! 별의 물방울 찾고 가세요!!





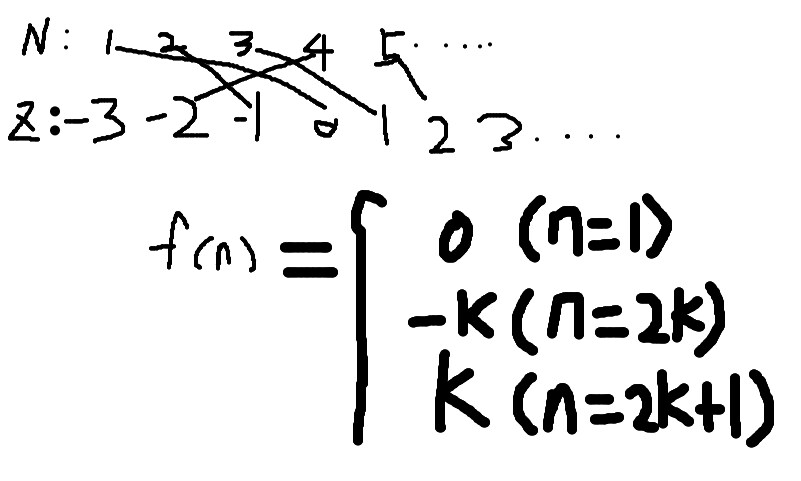





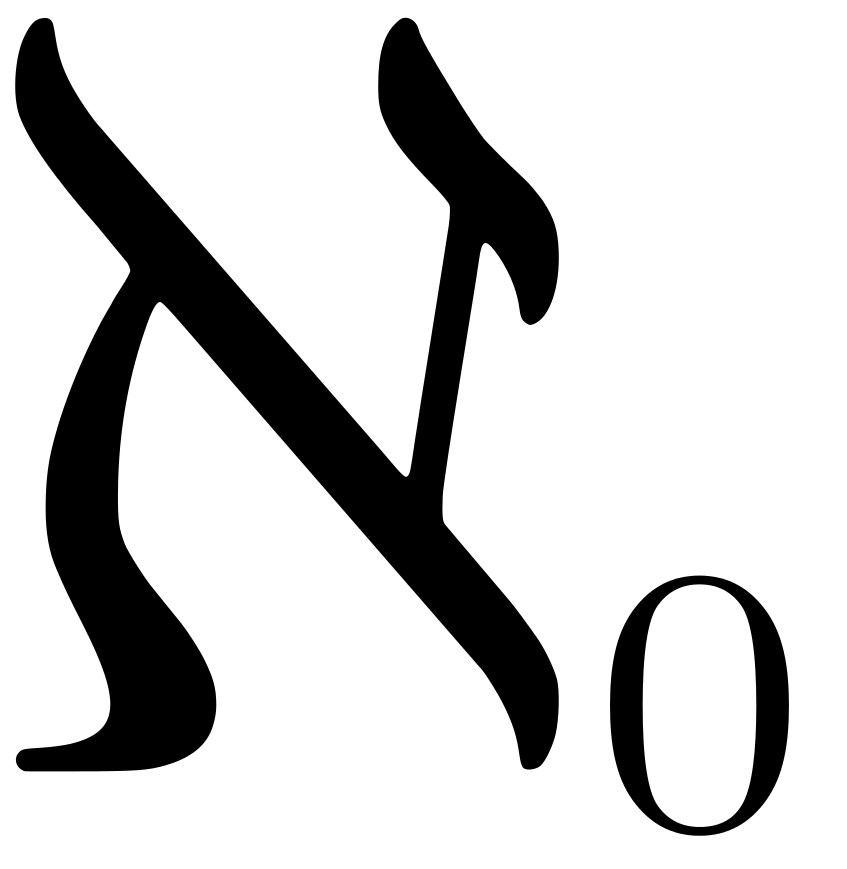
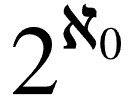








이왕 야레야레 하실거면 폴 코언 사진도 옆에 같이!